2021 數感嘉年華 之 挑戰珠立方

Bead-Chain Building Blocks

Contained within the box is a bead chain cube, showcasing an innovative method for building tensile structures. This wooden model utilizes four pre-tensioned linear bead chains interconnected with suitable cross-links. The elastic properties of the bead strings generate tension, causing the beads to repel each other when tightened. This interaction between string tension and bead repulsion ensures the overall self-balancing of the structure.

Bead-Chain Cube (BC-Cube):

Take apart BC-Cube to obtain four chains of five beads each.

Challenge 1: BC-Cube

The first task is to reconstruct the four five-bead chains into a cube structure as depicted in the diagram below. The eight terminal beads of these chains align with the vertices of the cube, while the remaining twelve beads are distributed along the cube's edges.

Challenge 2: Giant Tetrahedron

The next task is to link the same four five-bead chains into a tetrahedral arrangement as shown in the diagram below. Each edge of the tetrahedron consists of four beads, and each triangular face contains a total of ten beads.

Basic Operation

The fundamental process in constructing a bead chain model involves "cross-linking". As illustrated in the figure below with two chains of four beads each, the method entails stretching and crossing these chains over the gap between beads. The pre-stressed elastic strings create tension, causing the beads to snugly tighten and wrap around the crossing point.

Bead-Chain Molecular Models

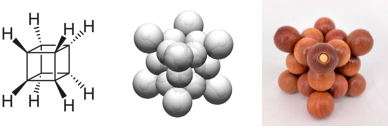
Bead-chain building blocks enable the construction of valence sphere models for various molecules. In these models, beads symbolize the valence electron pairs of the molecule, while the taut elastic strings provide the necessary attractive force to bind these electron pairs together within the molecule. By carefully balancing tension and compression, bead-chain building blocks effectively simulate the equilibrium structure of numerous molecules.

Cubane, with the chemical formula C₈H₈, features carbon atoms located at the eight vertices of a cube. These carbon atoms are bonded together by twelve carbon-carbon bonds, with the carbon-hydrogen bonds oriented outward from the structure.

See Also

• Chinese(中文)：珠串組合益智積木與珠立方
• Chinese(中文)：2021 數感嘉年華 之 挑戰珠立方 poster

External links

• 2019 Bridges Conference Art Exhibition: BC-Cube and BC-Dodecahedron by Bih-Yaw Jin
• Bih-Yaw Jin, Bead-Chain Construction Set and Interlocking Puzzle Inspired by Polyhedranes, Proceedings of Bridges 2019: Mathematics, Art, Music, Architecture, Education, Culture, 553–556.
• 2024 Bridges Conference Art Exhibition: Polyhedrane with Great Rhombicuboctahedron Skeleton and Bead-Chain Buckyball by Bih-Yaw Jin
• 2020 Bridges Conference Art Exhibition: Octahedral nanodiamond by Bih-Yaw Jin and Chia-Chin Tsoo
• 2021 Bridges Conference Art Exhibition: Bead-Chain Woven Sodalite by Bih-Yaw Jin
• 2022 Bridges Conference Art Exhibition: Interlocked Bead-Chain Model of Zeolite A Structure by Bih-Yaw Jin
• Facebook: 珠璣幾何 GeoBeading

Another dodecahedrane

I made one more valence sphere model (VSM) of dodecadrane (C₂₀H₂₀) yesterday. Although this model looks simple compared to other bead models I have made, I still feel satisfied every time I made a bead model of this molecule.

Styrofoam ball/rubber band model of ethylene

I posted a bead model of ethylene made by Qing Pang, a high-school student in TFG school. I don't like the way double bond is handled in her model because the channel (hole) orientations of two beads that used to model double bond is perpendicular to the bond orientation. I would prefer to have a bead valence model in which channel of each bead lies exactly along a particular bond. In the sense, to describe a double bond by beads, we need to use the banana bond representation of double bond proposed by Linus Pauling. This also means that, to construct a correct bead valence bond model of a double bond, we have to use a bead with a curved channel with an angle about 71 degree. I don't think one can get commercial beads which have channels with this particular angle.

But to illustrate the idea of banana bond, here I try to make a styrofoam ball/rubber band model of ethylene by carefully puncturing a channel with approximately this angle (see the styrofoam ball in the center). The resulting styrofoam model of ethylene looks just great!

It is straightforward to construct valence sphere model of acetylene with five styrofoam balls. Three of these balls represent triple bond and the remaining two balls represent single C-H bonds. Using the elementary geometry, one can show that the angle of the curved channel for the ball representing triple bond is about 38 degrees.

Styrofoam ball/rubber band model

Bead models can be viewed as a kind of valence sphere models (or tangent sphere models 價球模型或是切球模型), in which beads represent electron pairs. Similar idea using styrofoam balls and rubber band has been exploited in the 60s by L. Carrol King, a chemistry professor in the Northwestern university. Here is the first styrofoam ball/rubber band model of methane that I made.

Many people use this model to illustrate the valence sphere electron repulsion theory (VSEPR) for molecules with four valence electron pairs. We can easily see that the energy of the model in the square planar configuration is higher than that in the tetrahedral configuration. But one has to be careful in the interpretation because the energy difference in the total energy of these two configurations is from the elastic energy of the rubber band, instead of the repulsion energy among four hard spheres.

Twistane

I just learned a kind of molecule called twistane the other day. It looks so interesting and I decided to make a bead model for it.

Prismane

Prismane with 3-, 4-, and 5-fold rotational symmetry:

The hydrated diacetates of rhenium

The cover of the inorganic chemistry by J. E. House shows the structure of the hydrated diacetates of molybdenum(II), chromium(II), and rhenium. One can make a very good bead valence sphere model of this molecule containing a metal-metal bond.

Bead valence sphere model of penta-prismane

The structure of a penta-prismane is similar to that of a cubane. Instead of 4-fold rotational symmetry, one has a five-fold rotational symmetry. So the shape of penta-prismane is just like a pentagonal prism.

Bead valence sphere model of tetra-t-butyl tetrahedrane

The tetrahedrane derivative with four tert-butyl substituents, tetra-t-butyl tetrahedrane, was synthesized by the Austrian chemist,Günther Maier, in 1978. Here is the bead valence sphere model of this interesting molecule I made this afternoon. I think the hardest part to make molecules with many sp3 centers how to control the force evenly in the whole weaving process.

Pagodane （塔烷）

According to the wiki:

A pagoda （塔） is the general term in the English language for a tiered tower with multiple eaves common in Nepal, India, China,Japan, Korea, Vietnam, Burma and other parts of Asia. (source: wiki)

About twenty years ago, H. Prinzbach was able to synthesize an organic compound with a skeleton which resembles a pagoda by a 14-step sequence starting from isodrin. Thus he named the compound pagodane （塔烷）.

I just knew this molecule from the book "Molecules With Silly Or Unusual Names" by Paul W. May the other day. So here is the bead model of this interesting molecule.

Adamantane (金剛烷)

I made a bead valence sphere model of adamantane (chemical formula C₁₀H₁₆), which is a cycloalkane and also the simplest diamondoid.

Neopentane

Neopentane, also called dimethylpropane, is a double-branched-chain alkane with five carbon atoms. (from wiki)

Fullerane: C60H60

Fullerane is any hydrogenated fullerene or fully saturated fullerene. For instance, the fully saturated C₆₀ is C₆₀H₆₀. One can make a faithful valence sphere model of C₆₀H₆₀ with beads. The 150 beads in this model represent 300 valence electrons (240 from carbon and 60 from hydrogen) in this molecule.

Bead VSM of tetrahedrane

I should forget another platonic alkane, the tetrahedrane. The shape of this molecule based on the valence sphere model is just like 10 spheres close packed in a tetrahedron. Which models, valence sphere model or ball-and-stick model, is closer to the true shape of a tetrahedrane molecule?

Bead VSM of dodecahedrane

In principle, we can make the valence sphere model for any molecule with beads. But in practice, it is a little bit hard to thread the Nylon cord through a bead structure with tetravalent bonds, which are common for most molecules though.
But anyway, I made a bead VSM of dodecahedrane, C₂₀H₂₀.

Bead VSM of cubane

I just made a bead VSM (valence sphere model) of cubane (C₈H₈) by myself. The structure looks neat to me. Every valence electron pair is faithfully represented by a big bead, purple for CC bond and pink for CH bond. Small beads which have no chemical meaning are used to bind the pink beads to the central carbon cube. I didn't distinguish CC bonds from CH bonds. In principle, electron pairs responsible for these two types of chemical bonds should have different momenta. So they should have different sizes of charge clouds.

Bead VSM of methane, ammonium, water, and hydrogen fluoride

There is no doubt that tetravalent molecules such as methane occupy an important place in the chemical bond theory.
In 1865, German chemist August Wilhelm von Hofmann made the first stick-and-ball molecular models of methane in lecture at the Royal Institution of Great Britain. It is planar!

Then, 1872, van't Hoff, then a graduate student, learned of a possible tetrahedral arrangement of the valence bonds of carbon, proposed by the Russian chemist Alexander Butlerov in 1862. He later made a set of 3-D paper models of tetrahedral molecules.

Following Prof. H. Bent's recipes, Qing Pang (龐晴) of TFGH (北一女) made several bead valence sphere models (bead VSM) for tetravalent molecules with the formula AX_nE_m, where n+m=4, n is the number of bond electron pairs and m is the number of lone electron pairs. Here she didn't use the Windsor's knot to end the Nylon thread, instead she used simply tiny beads to cap the terminal beads of this kind of tree-like structures. Also, she use blue beads to represent bond electron pairs and yellow beads long electron pairs. You can see bead model exactly realizes the valence sphere model of Bent. I will show other bead VSM (made by Qing Pang) of molecules with several centers later.

Tangent sphere model of ethane

Using beads, one can make a faithful representation of the so-called valence sphere model (VSM) or tangent sphere model for a molecule proposed by Prof. Henry Bent in the 60s. In this model, each valence electron pair in a molecule is represented by a sphere. Its diameter is determined by the de Broglie wavelength of the corresponding electron, λ = h/p, where p is its momentum and h is the Planck constant.

Here is the first bead VSM (BVSM) of ethane (C₂H₆) made by Qing Pang (龐晴) of the Taipei First-Girls High School (北一女). She used the so-called Windsor-knot technique (雙活結) to bind beads that are not parts of loops in a molecular graph. For simplicity, she used beads of the same size to build the BVSM of ethane. This is equivalent to making the assumption that all valence electrons have the same momentum. The paper below the bead model is from the manuscript entitled "Approximate Molecular Electron Density Profiles. I. Construction" that I got from Prof. Bent last month.

BTW, Prof. Bent has just published a new book entitled "Molecules and the chemical bond" which is the first book-length sequel of his early articles on tangent sphere model last year. If you want to know more about the tangent sphere model, you should read the book or the original articles published in J. Chem. Edu.
You can read parts of this book at the google book.

1. Bent, H. A. J. Chem. Edu. 1965, 40, 446.
2. Bent, H. A. J. Chem. Edu. 1965, 40, 523.
3. Bent, H. A. J. Chem. Edu. 1967, 42, 308.
4. Bent, H. A. J. Chem. Edu. 1967, 42, 348.
5. Bent, H. A. J. Chem. Edu. 1968, 44, 512.
6. Bent, H. A. J. Chem. Edu. 1967, 45, 768.

Color pattern and VB structure

I recently communicated with Prof. Gillespie about the bead model of fullerenes. He raised a few questions on the way I interpreted the hard-sphere repulsion and its connection to the VSEPR (Valence shell electron pair repulsion) theory for AX₃ systems. (Even though, I am trying hard to convince him that this correspondence with suitable interpretation of beads. He still doesn't think bead model provides an example of VSEPR.) Through the discussion with him, I was inspired to look at the meaning of color beads more carefully.

In all of my previous bead models, I adopted a simple color scheme which is basically using a different color for each kind of nonhexagons. For a shared edge between a hexagon and a nonhexagon, we use nonhexagon's color for that shared edge.


However, we can also adopt a color scheme which has more chemical meaning simply by assigning one color to single bonds and another color to double bonds. From elementary chemistry, we know that each carbon atom has four valence electrons and should form four chemical bonds with its three neighbored carbon atoms in a fullerene. So we should also impose the following rules for arranging single and double bonds to satisfy the correct electron counting and molecular stability:

1. Surrounding each carbon atom, there are four electron pairs corresponding to two single bonds, and one double bonds, which can be represented by two white beads and one red bead, respectively.
2. Two connected double bonds (neighbored red beads) are strictly forbidden.
3. Three single bonds surrounding a central carbon atom will have an extra electron left without bonding and should correspond to a radical. This pattern is not energetically unfavorable and should be avoided either.

Each particular arrangement of single and double bonds correspond to the so-called valence bond (VB) structure. Usually, many VB structures can be found for a particular fullerene. A simple rule of thumb from quantum chemistry is that the more VB structures a fullerene has, the more stable the corresponding fullerene is. The ground state wave-function of the fullerene can be approximately expressed as a superposition of these VB structures.

Finding and enumerating all possible arrangements of single (white beads) and double bonds (red beads) in a fullerene with the above constraints is nontrivial.

As I have pointed out, the color pattern of C60 generated by the color scheme we used before corresponds to the most important VB structure of C60. Basically, in this VB structure, each of 12 pentagons consists of five single bonds and each of 20 hexagons consists of single and double bonds alternatively. One can in principle generate many more VB structures by rotating the single- and double-bond pattern in any of hexagons by one bond unit. This transformed hexagon is another Kekule structure of that hexagon.





In addition to C60, I just constructed a bead model of C70 with a color pattern in consistent with one of its VB structures. It is not hard to see the beautiful labyrinth pattern for this particular color scheme. Although I don't have a proof, I suspect the generality for the existence of labyrinth pattern in the bead model (using this color scheme, of course) of any fullerene without free radical, i.e. carbon only with three single bonds (white beads in the following picture).


A particular VB structure (resonance form) of C70:


The corresponding bead model with a colored VB pattern: