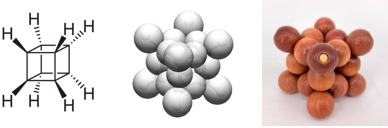
Contained within the box is a bead chain cube, showcasing an innovative method for building tensile structures. This wooden model utilizes four pre-tensioned linear bead chains interconnected with suitable cross-links. The elastic properties of the bead strings generate tension, causing the beads to repel each other when tightened. This interaction between string tension and bead repulsion ensures the overall self-balancing of the structure.
Bead-Chain Cube (BC-Cube):
Take apart BC-Cube to obtain four chains of five beads each.
Challenge 1: BC-Cube
The first task is to reconstruct the four five-bead chains into a cube structure as depicted in the diagram below. The eight terminal beads of these chains align with the vertices of the cube, while the remaining twelve beads are distributed along the cube's edges.
Challenge 2: Giant Tetrahedron
The next task is to link the same four five-bead chains into a tetrahedral arrangement as shown in the diagram below. Each edge of the tetrahedron consists of four beads, and each triangular face contains a total of ten beads.
Basic Operation
The fundamental process in constructing a bead chain model involves "cross-linking". As illustrated in the figure below with two chains of four beads each, the method entails stretching and crossing these chains over the gap between beads. The pre-stressed elastic strings create tension, causing the beads to snugly tighten and wrap around the crossing point.
Bead-Chain Molecular Models
Bead-chain building blocks enable the construction of valence sphere models for various molecules. In these models, beads symbolize the valence electron pairs of the molecule, while the taut elastic strings provide the necessary attractive force to bind these electron pairs together within the molecule. By carefully balancing tension and compression, bead-chain building blocks effectively simulate the equilibrium structure of numerous molecules.
Cubane, with the chemical formula C
8H
8, features carbon atoms located at the eight vertices of a cube. These carbon atoms are bonded together by twelve carbon-carbon bonds, with the carbon-hydrogen bonds oriented outward from the structure.
See Also
External links