虧格31的超級巴克球 Super Buckyball of Genus 31

聯合數學會議（Joint Mathematics Meetings, JMM）是世界上最大的數學學術會議之一，除了數學研究的交流，會議的藝術展覽也提供了一個獨特的平台，展示數學與藝術之間的奇妙聯繫。在 **2013 年的聯合數學會議**上，一件名為 "**Super Buckyball of Genus 31**" 的藝術品吸引了眾多目光。

背景介紹：富勒烯與拓撲虧格

在欣賞這件藝術品之前，我們先簡單了解一下相關的背景知識：

• 富勒烯（Fullerene）： 富勒烯是一類完全由碳原子組成的中空的球狀、橢球狀、或管狀分子。最著名的富勒烯是 **C60，又稱足球烯或巴克球（Buckyball）**，其結構與足球相似，由 20 個六邊形和 12 個五邊形構成。
• 拓撲虧格（Genus）： 在拓撲學中，一個曲面的虧格是指它包含的“洞”的數量。例如，一個球面（如普通的巴克球）的虧格為 0，而一個環面（如甜甜圈）的虧格為 1。**Genus 31** 意味著這個結構在拓撲上相當複雜，擁有 31 個“洞”。

藝術品詳情：Super Buckyball of Genus 31

Super Buckyball of Genus 31

創作者：**金必耀 (Bih-Yaw Jin) 及台北第一女子高級中學的師生**

• 尺寸： 20 英寸 x 20 英寸 x 20 英寸（約 60 厘米 x 60 厘米 x 60 厘米）
• 材料： 塑料珠子
• 創作年份： 2011

這件 "**Super Buckyball of Genus 31**" 是一個使用塑料珠子製作的大型多面體模型。它並非一個普通的巴克球（Genus 0），而是一個 **虧格為 31 的超級巴克球**。

這個模型的每一個頂點本身都是一個帶有三個孔的巴克球，並且通過三個最短的碳納米管連接到三個相鄰的頂點。

另一種理解這個結構的方式是將其視為第二層的 Sierpinski 巴克球，並且這種結構可以無限擴展。Sierpinski 結構是一種分形，通過不斷地自我複製和縮小形成複雜的圖案。將 Sierpinski 的概念應用於巴克球，創造出更複雜、更高虧格的結構，體現了數學中迭代和自相似性的思想。

這件藝術品是由金必耀教授與台北第一女子高級中學的師生於2011 年 11 月共同製作完成的。這也展現了數學和科學概念在教育和公眾推廣中的藝術表達。

通過將抽象的數學概念（如拓撲虧格和分形）與具體的物理模型相結合，"Super Buckyball of Genus 31" 不僅是一件引人注目的藝術品，也是探索複雜幾何結構的一種有趣方式。

參考資料

• Bih-Yaw Jin | 2013 Joint Mathematics Meetings | Mathematical Art Galleries: #### Artworks ##### Super Buckyball of Genus 31. 2013 Joint Mathematics Meetings Bih-Yaw Jin

© 2025 珠璣科學｜Super Buckyball of Genus 31

Bead models of four Archimedean solids

Truncated octahedron, truncated icosahedron (C₆₀), truncated cuboctahedron (great rhombidodecahedron), truncated icosidodecahedron (great rhombicosidodecahedron):

C60's bead models for the International Chemistry Olympiad 2015, Azerbaijan

I am a member of Taiwan Chemistry Olympiad team for the 2015 IChO (International Chemistry Olympiad) which will be held next week at Baku, Azerbaijan. We prepared many C60 bead models as souvenirs for participants from around the world. To make about 200 bead models of C60. we got help from chemistry teachers and many senior students of the Taipei First-Girl School (TFGH). Most of these students have just got acceptances from colleges and have some spare time to help us prepare these beautiful bead models.

However, it is fun to make one's own beaded C60, so Chia-Chin and I also prepared about 200 kits of materials and detailed instruction for making C60.

A few photos from the NTU Chemistry Camp

I gave a workshop for the summer chemistry camp of the chemistry department at the National Taiwan University early this month. This is a summer camp for the local high school students. There are about 60 participants this year. Here a few photos from the workshop:

The title and the first slide of my workshop for the chemistry summer camp:

Evolution of superbuckyballs

Since the last month of 2011, I started to work on the so-called Sierpinski buckyballs or superbuckyballs, which belong to a particular family of fullerenes created by treating C60s as supernodes and carbon nanotubes as superbonds. Using this idea, an unlimited number of hierarchical super-structures of sp²-hybridized (3-coordinated) carbons can be constructed. Before this task was really started, I have managed to build some simpler structures such as super-triangle, super-tetrahedron, and other related structures. With the experience, I firmly believed in the feasibility of creating bead models of much larger superbuckyballs. But it is too tedious to construct bead models for this kind of super-structures, especially the so-called C60xC60, alone. So I designed a modular approach to build these models collaboratively. I told a few chemistry teachers, especially Dr. Chou (周芳妃), at a local high school, The Taipei First-Girl School (TFGH), about this structure. They were glad to try this idea out together. The results are two beautiful superbuckyballs (or C60xC60) made by 6mm and 12 mm beads, respectively. Both of the structures were on public display for the anniversary of TFGH and a simultaneous event of the TFGH's 30-year alumni reunion. Alumni association of TFGH kindly supported the whole project. Dr. Tsoo was one of alumni that year, that was why we got supported from them.

Later on, I made another bead model of C60xC60 for the JMM held in San Diego about two years ago (Jan. 2013). I used the photo of the giant bead model students and I made in the JMM description though. I met Chern (莊宸) in the meeting. We discussed the structural rules for this family of compounds. Particularly, I commented on that the particular model I made cannot be constructed by Zometool. After returning back to Cambridge, MA, Chern solved the problem by carefully puncturing holes along certain symmetry axes in order to be consistent with the Zometool requirements.

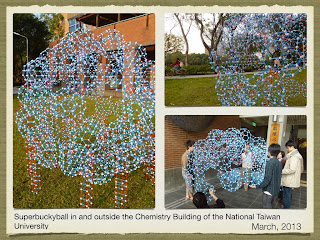
Yuan-Jian Fan (范原嘉) then proved Chern's idea by building a virtual C60xC60 super-buckyball with the zometool construction software, vZome, which was kindly given to us by its author, Scott Vorthmann, a few years ago. With everything ready, a few enthusiastic students from the theoretical chemistry group of the National Taiwan University started to build the first zometool super buckyball after the Chinese new year.

Soon, a number of practical issues on the construction of a real zometool model of C60xC60 super-buckyball appeared. The first issue is the structural stability against gravity. The original neck structures (shortest situations) designed by Chern consisted of a number of octagons were too weak and simply cannot hold the whole structure due to its own weight. Another issue is still weight, without extra stands, the southern hemisphere of super-buckyball constructed by zometool simply cannot hold the northern hemisphere. Finally, how to put those parts on top without scaffold is also a question. All these problems were solved beautifully by Yuan-Jia Fan. Of course, local dealer, Helen Yu, of Zometool in Taiwan is also helpful. She always responded us with the necessary zometool pieces upon our requests in a very short time. So, we can have the first zometool sculpture of C60xC60 erected in the NTU campus around mid-March.

Chern then proposed to Paul Hildebrand to have a family-day activity for the 2013 Bridges which will be held in Enschede that year. Paul agreed to provide us with the necessary materials. At the family day, we got more help from a few Bridges participants and their family members from Taiwan. These included Profs. Liu (劉柏宏) and Tung-Shyan Chen (陳東賢). Without them the final C60xC60 structure couldn't be finished in such a short period.

In addition to the construction of huge zometool superbuckyball, Chern also presented a small bead model to the Bridges meeting as shown in the following pictures based on the same construction rule he designed. Another bead model in his right hand is an edge-elevated dodecahedron assembled from fifty C80s, twenty for the vertices of dodecahedron and thirty for the elevated edges. The idea for making this one is similar to C60xC60. I brought them back to Taiwan and put them on exhibition in the NTU Chemistry Museum for about a year until the last July when Chern got an email from George Hart asking him about the possibility of donating this small C60xC60 model for MoSAIC (Mathematics of Science, Art, Industry, and Culture) traveling exhibition. In the email, George commented on this model as " having the right combination of artistic expression, mathematical content, and practical transportability".

The Brazuca and octahedral fullerenes

Yuan-Jia and I submitted a manuscipt entitled, From the "Brazuca" ball to Octahedral Fullerenes: Their Construction and Classification, to the physics preprint archive, arXiv, recently. Basically, we observed that the symmetry of the Brazuca ball used in the FIFA World Cup held now in Brazil is exactly that of an octahedral fullerene, which Yuan-Jia has been thinking about for more than a year. Therefore, we modified the original manuscript a little bit to point out this peculiar connection. Hopefully, researchers can know that not only the original the Adidas Telstar, a truncated icosahedron, has a microscopic analog, namely the famous C₆₀, the current Brazuca ball could also have microscopic correspondence, in principle.

The Adidas Telstar vs a C₆₀ molecule

The Adidas Brazuca vs an octahedral fullerene

Here I give a list of symmetry groups for all official match footballs (soccer balls) adopted by the FIFA since 1970:

Year	Country	Name of the official match ball	Point group
1970	Mexico	The Adidas Telstar	Ih
1974	West Germany	The Adidas Telstar Durlast	Ih
1978	Argentina	The Adidas Tango Durlast	Ih
1982	Spain	The Adidas Tango Espana	Ih
1986	Mexico	The Adidas Azteca	Ih
1990	Italy	The Adidas Etrvsco	Ih
1994	USA	The Adidas Questra	Ih
1998	France	The Adidas Tricolore	Ih
2002	Korea Japan	The Adidas Fevernova	Ih with T pattern
2006	Germany	The Adidas Teamgeist	Th
2010	South Africa	The Adidas Jabulani	Td
2014	Brazil	The Adidas Brazuca	O

It is interesting to note that it took FIFA 28 years to move away from the icosahedral symmetry to the tetrahedral symmetry, and then another 12 years to come to the last of three Platonic symmetry groups, namely the octahedral group. Another peculiar difference between the Brazuca ball and the previous soccer balls is the lack of inversion and mirror symmetries in the Brazuca ball, meaning that the Brazuca ball is chiral. This should lead to nonvanishing coupling between translational and rotational (spinning) motions, I suspect.

C60 and T120 with 5mm cateye stones

It's been a while since I made T120 and C60 sometime ago. Also, I have given away all other cateye T120 models made by Chern many years ago. Hopefully, I can show more models with this kind of beads in the future.

Giant beaded buckyball

I went to the 109th anniversary of TFGH yesterday and took a photo of this interesting giant buckyball.

Coalescence of two or more C60s

Previously, I constructed many large graphitic structures by fusing C60 along a particular 5-fold axis. But in addition to the 5-fold axes, one can also fuse two C60s along a particular 3-fold axis to get different kind of fused structures. One can easily see that the topological charges of necks in these two structures are the same, i.e. (-1)x6=0x3+(-2)*3=-6. The total topological charges are, of course, equal to 18x1+(-6)=12. However the relative arrangement for the two C60s are different, staggered for the pure-heptagon neck, while eclipsed for the hexagon-octagon neck. In fact, Diudea and Nagy have already done a lot on this possibility. Read the book for more information.

The following two pictures show two possible ways of coalescence: the neck of the first one consists of a ring of octagons and hexagons alternatively; the second one is a ring of six heptagons, instead.

In principle, one can create a one-dimensional tube by coalescence of many C60s repeatedly.

Two gifts from Mr. Horibe

I am usually the person who gave people beadworks as gifts. But I myself got a beaded C60 as a gift from Mr. Horibe on our visit to his home. And the next day, when he participated my workshop in Nagoya, I got another giant torus as a gift.



His model is quite different from mine because most often he used only a single elastic rubber band with exact length to make his beadworks. In this sense, the path of his elastic string exactly corresponds to the Hamiltonian path exactly and has, of course, the minimal length for a particular model. So, the elastic string passed every bead in the model twice and only twice. To avoid beads fall apart, Mr. Horibe then made a knot in the end. So you can pull or press his bead models to some extent.



Possibly due to his training as mathematics teacher, he always uses a single string even for structures that contain more several thousand beads. I was quite surprised when I just heard of it. Just imagine how one can use a single string to bead the giant green stellated dodecahedron as shown in the following photo. The problem is that it would become very difficult to bead with such a long string. The good thing is that the path of string in his case is really a Hamiltonian path no matter how many beads a model contains. I guess that he also needed to plan well before he started because it is not always trivial to find out the Hamiltonian path. Sometimes, we just got trapped as weaving process goes. I don't know how he managed to do it with only one string especially for certain structures that has more than several thousand beads.



Another practical aspect about using elastic string is that elastic string is much thicker than the Nylon string I typically used. I suspect that it may not easy to pass it through three times through a hole. But of course, it is not a good idea to pass string through some beads twice, but some other beads three times because that will make the tension generated by the rubber band uneven throughout the structure. There is no such problem for the Nylon string because the bead models made by Nylon string are usually quite strong and hard. So it is harder to deform them like the model made with elastic rubber band.

Construction procedure of C60 (Japanese translation)

Prof. Sonoda made a nice Japanese translation of the detailed construction described in the supporting information of the article, Molecular Modeling of Fullerenes with Beads, J. Chem. Edu 2012 , 89 (3), 414–416.", by Prof. Cuccia and me.



Also, here is the original English version of the first page, the next two pages are the same.

Japanese translation of 珠璣科學─串珠碳六十

Prof. Inoue (井上吉教) of Hikone prefecture university and one of his Chinese students kindly translated my article "珠璣科學─串珠碳六十" (The Science of Beading - Beaded C60) with Dr. Tsoo for the March issue of the "Science Monthly (科學月刊)" magazine.



(New post, scanned images 6/12/2012)


Prof. Inoue also made a few fullerenes as shown in the following pictures. I didn`t check them very carefully. Possibly, one of them is the icosahedral C80 and another is the cylindrical shape C84. There seems　to be a fullerene belonging to D_3h point group.

Two more resonance structures of C60

As I mentioned before, two chemists, Vukicevic and Randic, gave a complete enumeration of all possible resonance forms in their paper, Detailed Atlas of Kekulé Structures of the Buckminsterfullerene, in "The Mathematics and Topology of Fullerenes". According to them, there are 158 irreducible Kekule structures for C₆₀. Following the Schlegel diagrams listed in the paper, one can easily make a bead model for any resonance structure.

I found these two intriguing resonance forms, No. 108 and 111, of C₆₀ quite accidentally yesterday. Although I knew the existence of No. 108 for a long time, I didn't know No. 111 before. I also suspect they might be the only two resonance structures which have patterns of parallel stripes along the latitude coordinates. Particularly, the Kekule structure 108 has a 5-fold rotational symmetry axis with two pentagons located at two poles and the Kekule structure 111 has a 3-fold rotational symmetry instead.

Three Kekule structures of C60

D. Vukicevic and M. Randic have figured out all possible distinct resonance (or Kekule) structures a few years ago. According them, buckminsterfullerene has 12500 Kekule structures grouped in 158 isomorphic classes. They also give a complete list of all these 158 non-isomorphic Kekuke structures in a recent paper entitled "Detailed Atlas of Kekulé Structures of the Buckminsterfullerene", in the book, "The Mathematics and Topology of Fullerenes".

This is very convenient if we want to make any particular resonance form of C₆₀. We can simply look at the Schlegel diagrams given in this paper, and pay attention to the single and double bond pattern as we bead. Here are three bead models for Kekule structures No. 134, 135 and 136 as shown in their paper.

Making Beaded Buckyball Model in Chinese

If you can read Chinese, you might want to look at the following detailed tutorials by a teacher, 薛朋雨, at the Taichung First High School (國立台中第一高級中學):

化學教室活動：製作巴克球的串珠模型（Making Beaded Buckyball Model）〔I〕
化學教室活動：製作巴克球的串珠模型（Making Beaded Buckyball Model）〔II〕
化學教室活動：製作巴克球的串珠模型（Making Beaded Buckyball Model）〔III〕

Another Resonance Structure of C60

Wikipedia has a resonance structure of C60 in its "Buckminsterfullerene" item. I made a bead model with color code according to this resonance form last weekend. Again one can see the interesing pattern of this resonance structure. Also white beads (or single bonds) form a long connected one-dimensional loop.

I also tried to make another resonance structure by only paying attention to the local condition. But at the last loop, I found that I couldn't satisfy the local condition any longer. So I used a red bead to show this frustration.

Bead models in the corridor of TFGH

I went to the Taipei First Girls High School (TFGH) a few times last week to work on the super Buckyball with chemistry teachers and students. Outside the teachers' office, there are a number of beautiful bead models hung right under the corridor ceiling. Many students also wrote their wishes on paper strips attached to their models. Many of them are quite interesting and fun.

More information about the Taipei First Girls High School from wiki:
"Taipei First Girls' High School (臺北市立第一女子高級中學) is a prestigious Taiwanese high school, located in Zhongzheng District within Taipei City, with only the top 1% of scorers on the Basic Competence Test for Junior High School Students (國民中學學生基本學力測驗) receiving admission."