C60's bead models for the International Chemistry Olympiad 2015, Azerbaijan

I am a member of Taiwan Chemistry Olympiad team for the 2015 IChO (International Chemistry Olympiad) which will be held next week at Baku, Azerbaijan. We prepared many C60 bead models as souvenirs for participants from around the world. To make about 200 bead models of C60. we got help from chemistry teachers and many senior students of the Taipei First-Girl School (TFGH). Most of these students have just got acceptances from colleges and have some spare time to help us prepare these beautiful bead models.

However, it is fun to make one's own beaded C60, so Chia-Chin and I also prepared about 200 kits of materials and detailed instruction for making C60.

Hyperbolic buckyball

拍攝時間：2015/4/28; 地點：北一女
作品完成時間：2015/2/8

Evolution of superbuckyballs

Since the last month of 2011, I started to work on the so-called Sierpinski buckyballs or superbuckyballs, which belong to a particular family of fullerenes created by treating C60s as supernodes and carbon nanotubes as superbonds. Using this idea, an unlimited number of hierarchical super-structures of sp²-hybridized (3-coordinated) carbons can be constructed. Before this task was really started, I have managed to build some simpler structures such as super-triangle, super-tetrahedron, and other related structures. With the experience, I firmly believed in the feasibility of creating bead models of much larger superbuckyballs. But it is too tedious to construct bead models for this kind of super-structures, especially the so-called C60xC60, alone. So I designed a modular approach to build these models collaboratively. I told a few chemistry teachers, especially Dr. Chou (周芳妃), at a local high school, The Taipei First-Girl School (TFGH), about this structure. They were glad to try this idea out together. The results are two beautiful superbuckyballs (or C60xC60) made by 6mm and 12 mm beads, respectively. Both of the structures were on public display for the anniversary of TFGH and a simultaneous event of the TFGH's 30-year alumni reunion. Alumni association of TFGH kindly supported the whole project. Dr. Tsoo was one of alumni that year, that was why we got supported from them.

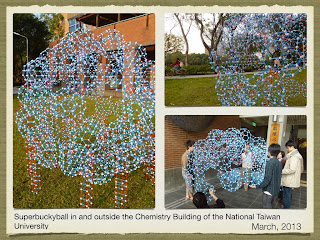
Later on, I made another bead model of C60xC60 for the JMM held in San Diego about two years ago (Jan. 2013). I used the photo of the giant bead model students and I made in the JMM description though. I met Chern (莊宸) in the meeting. We discussed the structural rules for this family of compounds. Particularly, I commented on that the particular model I made cannot be constructed by Zometool. After returning back to Cambridge, MA, Chern solved the problem by carefully puncturing holes along certain symmetry axes in order to be consistent with the Zometool requirements.

Yuan-Jian Fan (范原嘉) then proved Chern's idea by building a virtual C60xC60 super-buckyball with the zometool construction software, vZome, which was kindly given to us by its author, Scott Vorthmann, a few years ago. With everything ready, a few enthusiastic students from the theoretical chemistry group of the National Taiwan University started to build the first zometool super buckyball after the Chinese new year.

Soon, a number of practical issues on the construction of a real zometool model of C60xC60 super-buckyball appeared. The first issue is the structural stability against gravity. The original neck structures (shortest situations) designed by Chern consisted of a number of octagons were too weak and simply cannot hold the whole structure due to its own weight. Another issue is still weight, without extra stands, the southern hemisphere of super-buckyball constructed by zometool simply cannot hold the northern hemisphere. Finally, how to put those parts on top without scaffold is also a question. All these problems were solved beautifully by Yuan-Jia Fan. Of course, local dealer, Helen Yu, of Zometool in Taiwan is also helpful. She always responded us with the necessary zometool pieces upon our requests in a very short time. So, we can have the first zometool sculpture of C60xC60 erected in the NTU campus around mid-March.

Chern then proposed to Paul Hildebrand to have a family-day activity for the 2013 Bridges which will be held in Enschede that year. Paul agreed to provide us with the necessary materials. At the family day, we got more help from a few Bridges participants and their family members from Taiwan. These included Profs. Liu (劉柏宏) and Tung-Shyan Chen (陳東賢). Without them the final C60xC60 structure couldn't be finished in such a short period.

In addition to the construction of huge zometool superbuckyball, Chern also presented a small bead model to the Bridges meeting as shown in the following pictures based on the same construction rule he designed. Another bead model in his right hand is an edge-elevated dodecahedron assembled from fifty C80s, twenty for the vertices of dodecahedron and thirty for the elevated edges. The idea for making this one is similar to C60xC60. I brought them back to Taiwan and put them on exhibition in the NTU Chemistry Museum for about a year until the last July when Chern got an email from George Hart asking him about the possibility of donating this small C60xC60 model for MoSAIC (Mathematics of Science, Art, Industry, and Culture) traveling exhibition. In the email, George commented on this model as " having the right combination of artistic expression, mathematical content, and practical transportability".

Giant beaded buckyball

I went to the 109th anniversary of TFGH yesterday and took a photo of this interesting giant buckyball.

D- and G-types TPMSs

28 groups of students from TFGH joined the competition designed by Ms. Chou and other teachers in the chemistry group of TFGH. They were asked to make any of these two complicated 3D models based on the slides I prepared for the G- and D-surfaces. It is still nontrivial for a beginner, who has no knowledge on the periodic minimal surfaces and graphitic structures. But most of them succeeded in creaking one of these two models. Unfortunately, when they asked local sellers about the suitable thickness of Nylon strings for 12mm beads. They were told that 0.6mm NyLong strings are best. That is why most of models they made are so soft and unable to stand on themselves. To solve the problem, students came up with the idea to hang these models on four legs of an upside-down desk they use for lectures.

However, one group discovered the cause to be the thickness of the Nylon string. Then students of that group changed the Nylon strings to 0.8mm. The two TPMS models they made are shown in the following photo. They look really nice and beautiful.

The one on the left is the G-surface. The one on the right side is the D-surface consisting of 16 helical strips. Using the decomposition technique Chern Chuang designed, we can use the same helical strips to create these two types of TPMSs.

Gyroidal Invinciball

A graphitic gyroid is a hyperbolic object. To make it, we need to introduce octagons at suitable positions on a graphitic sheet, which is similar to the pentagons in the spherical space such as buckyball. In some sense, we can view graphitic gyroid as a kind of "ball" in the hyperbolic space.

Students from the TFGH created this gyroidal invinciball in the hyperbolic space. Unfortunately, they used 0.6mm Nylon strings for the 12mm faceted beads. The structure is too soft to stand on its own.

Gyroidal National Flag of Republic of China (Taiwan)

I went to a special ceremony for the beading competition held in the Tapei First Girls High School this afternoon. I saw this amazing 3D flag model of my country, Republic of China (i.e. Taiwan), which is made by a suitable color code of octagons in a gyroidal graphene.

BTW, you can also interpret this flag as that of US.

G- and D-surfaces in TFGH

Fang-Fei Chou and other teachers of chemistry section of the Taipei First Girl High school (TFGH) started a new bead project based on the slides I made for the anniversary of their school early next month. Using these slides only, they are going to make 2x2x2 G and D surfaces by themselves. Fang-Fei told me that there are about 30 teams in this project, which means they are going to have about 30 giant bead models of TPMS.

Attached is a photo that shows their current progress.

As you can see that their strips are quite long because they use 12mm beads. I made two G surfaces with 6mm and 8 mm beads, respectively. The one made of 6mm beads is about 20x20x20cm. So the G surfaces they are going to make are about 40x40x40cm. I wonder where they are going to put so many gigantic bead models.

The procedure for constructing G- and D- surfaces

Here are a few slides that show the detailed instruction for making G- and D- surfaces, which I prepared for students and teachers of TFG (Taipei) school. As I said it could be a difficult task because the gyroidal structure and D-type TPMS are complicated structures. The first bead model of a 2x2x2 G-surface took Chern and I almost five years to finally make it. Of course, I have many unfinished bead models of this structure or similar structures with different Goldberg vectors, some made by Chern and some by me, which have mistakes here or there.

In order to how to make this model successfully, we'd better to know the three-dimensional structures of G- and D-type surfaces a little bit. Additionally, it is crucial to know how two structures can be decomposed into several basic unit strips and how to connect these helical strips.

I am also working on an article in Chinese entitled "大家一起動手做多孔螺旋與鑽石型三度週期最小曲面的串珠模型 (A Hands-on, Collaborative Approach to Gyroid- and Diamond-type Triply Periodic Minimal Surfaces with Beads)", which describes in details the procedure to make G- and D-surfaces and also give some background information on TPMS. I might be able to finish the paper in a few days. Hopefully, I will find time to do it in English someday. But, even without detailed explanations, these slides together with other posts in this blog should already contain enough information for people who want to do it.

The first nine slides should give students a better picture of a gyroid:

In slide 10, we can see how a coronene unit corresponds to 1/8 unit cell. Important structural features of a beaded gyroid is summarized in slide 11. Then in slides 12-15, I describe how to make the basic construction unit, a long strip, which should be easy for student to make.

The remaining five slides, 16-20, use schematic diagrams to show how two slides can be combined to generate either D-surface or G-surface.

To create a 2x2x2 gyroidal surface, we need 16 strips, which can be easily done if many people work in parallel. To connect them is nontrivial, you need to follow slides 16-20 carefully. In total, there are about 5000 beads in the model.

P, G, and D surfaces

I am planning to have a project with students and teachers of TFG (Taipei) school later this month to construct Gyroidal and D surfaces together. It could be a difficult task because the gyroidal structure is probably the most complicated bead structure Chern and I have ever made. A simple tutorial on the three-dimensional structure of a gyroidal surface and how it can be decomposed into several basic and easily weaved units seems to be useful. So I am now preparing some slides to make the project work out smoothly. Here is one of the slides about the famous P-, D- and G-types Triply Periodic Minimal Surfaces (TPMS) which I generated with matlab:

Additionally, Chern, Wei-Chi, Chia-Chin and I also have a paper jointly for the Bridges meeting last summer. Chern made the presentation. I didn't attend it, though. This paper describes the bead models of these three structures quite generally.

Chuang, C.; Jin, B.-Y.; Wei, W.-C.; Tsoo, C.-C. "Beaded Representation of Canonical P, D, and G Triply Periodic Minimal Surfaces", Proceedings of Bridges: Mathematical Connections in Art, Music, and Science, 2012, 503-506.

photos from TFGH

Fan-Fei (周芳妃老師), chemistry teacher of the Taipei First-Girls' High School (TFGH), informed me a site with many pictures she and her colleagues took for several events from Nov. 9 to Dec. 11, 2011.

1. Nov. 9, 2011: students and teachers of TFGH attent my exhibition "The Fabulous World of Beaded Molecules" held in our department.

2. Nov. 28, 2011: Students of TFGH visited our department and I gave a talk "珠璣科學" for them.
3. Nov. 2-11, 2011: We collaborated on the superbuckyball.

Bead models in the corridor of TFGH

I went to the Taipei First Girls High School (TFGH) a few times last week to work on the super Buckyball with chemistry teachers and students. Outside the teachers' office, there are a number of beautiful bead models hung right under the corridor ceiling. Many students also wrote their wishes on paper strips attached to their models. Many of them are quite interesting and fun.

More information about the Taipei First Girls High School from wiki:
"Taipei First Girls' High School (臺北市立第一女子高級中學) is a prestigious Taiwanese high school, located in Zhongzheng District within Taipei City, with only the top 1% of scorers on the Basic Competence Test for Junior High School Students (國民中學學生基本學力測驗) receiving admission."

Super Buckyball (超級珠璣碳球)

After about ten days of hard working, we finally created this fabulous super Buckyball. I have to thank the alumni association of the Taipei First Girls High School (TFGH), especially the classes 1981, 1971, and 1961, who kindly sponsor this project and donate this super Buckyball to the TFGH as a gift from their 30-, 40-, and 50-years joint reunion.
Of course, the crucial collaborative effort of students (mainly from classes 2She (二射) and 2Yue (二樂)) and teachers of the TFGH makes this super Buckyball possible in about two weeks.

Explaining the weaving path to students:

Students working hard:

Super Buckyball (超級珠璣碳球)

The first super Buckyball, C₄₅₀₀, was created by students (class 3Gong 三恭) from the Taipei First Girls High School (TFGH) 北一女中 today. Each unit in this beautiful bead model is a punctured C60 with three holes surrounded by a neck of five heptagons. It took them exactly one week to construct it. The diameter of this small super Buckyball (made of 6750 6mm beads) is about 40 cm already. They might still need to clean all the loose ends up later next week.

In addition to this small super Buckyball, I am still working with teachers and some other students from the TFGH on a bigger super Buckyball made of 12mm beads. Hopefully, we can have the whole structure done early next week. Since the total weight of this model is going to be eight times of this small super Buckyball, so we need to be very careful about the rigidity of each units and necks connecting them. I name these kinds of bead models as "超級珠璣碳球" in Chinese which means literally "the super bead carbon ball".

(I found many pictures at TFGS's website. http://web.fg.tp.edu.tw/~chemistry/blog/?page_id=2&nggpage=8, 2012/9/1)

Building blocks for the type-II high-genus fullerenes

The building block of type-II high-genus fullerenes can be chosen to be an arbitrary Goldberg polyhedron. Puncturing three holes along three carefully chosen pentagons can create a basic unit with three coordination (or a trivalent unit).
I use C60 and its Schlegel diagram to illustrate how to puncture a hole on an arbitrary pentagon.

1. Schlegel diagram of C60

2. C60 with a hole punctured on a pentagon: one pentagon and five hexagons are replaced by five heptagons.

In principle, one can connect two this kind of unit with one hole to create a fused C120 with dumbbel-shape.

3. Of course, if we like, we can puncture two holes on a C60. There are three possible ways. Here I only show the situation with two pentagons separated by two hexagons. The resulting structure will contain two holes connected (or separated) by two heptagons.

There are two other different ways to puncture second hole. If the second pentagon separated from the first one by one CC bond are punctured, the resulting structure will have an octagon. The third situation is that the second pentagon is located at the antipodal position. I will talk about these situations later.

4. Punctured C60 with three holes:

It is easy to see that there are five heptagons and five more bonds are introduced around each hole. So one needs 105 beads for creating a single unit.

5. Here are two possible weaving path. I usually used the first path though. a. non-spiral path

b. spiral path

6. I am working on a project with teachers and students of the Taipei First Girls High School (北一女). We are going to make a giant buckyball consisting of sixty units of punctured C60s. Here are a few basic units I made:

105 12mm faceted beads are used for each unit.