探索非週期之美：手性向量 為(4,0)的串珠 馬凱二十面體

在 2014 年的 Bridges 會議上，金必耀與左家靜 共同展出了一系列令人著迷的數學藝術作品。其中一件名為 手性向量 為(4,0)的串珠 馬凱二十面體 「Beaded Mackay icosahedron with chiral vector (4,0)」 的串珠雕塑，以其獨特的幾何結構和精湛的工藝，吸引了眾多目光。

這件作品的尺寸為 18x18x18 厘米，於 2014 年 使用 3 厘米的空心玻璃珠 (3cm tubular Glass beads) 製作而成。從名稱中可以看出，這件藝術品的核心是一個 馬凱二十面體 （Mackay icosahedron）。

什麼是 馬凱二十面體 呢？

馬凱二十面體 是一種 準晶體的結構單元 (building units of the quasi-crystal)。 準晶體是一種 有序但不具週期性的結構，其獨特性在於 五重旋轉對稱性與平移對稱性之間存在不相容性。這與我們常見的晶體具有明確的週期性結構有所不同。馬凱二十面體 本身就呈現出類似二十面體的結構，但在原子或結構單元的排列上更為複雜。

金必耀與左家靜選擇以串珠的方式來呈現這種複雜的幾何體。他們運用了 角編織技術 (angle weave technique) ，將多種剛性多面體單元 連接 在一起，構建出這個 馬凱二十面體 。具體來說，這個串珠雕塑是由 四面體 (tetrahedra)、八面體 (octahedra) 和五角雙錐 (pentagonal bipyramids) 這三種多面體相互連接而成。

在最終的雕塑中，二十面體 (icosahedron) 的 20 個面是由四面體和八面體填充的，而五角雙錐則構成了這個 馬凱二十面體的 12 個頂點 (apexes)。這種精心的構造方式不僅在視覺上呈現了 馬凱二十面體的形態，也體現了其內部不同幾何單元之間的複雜關係。

透過這件手性向量 為(4,0)的串珠 馬凱二十面體 ，我們可以感受到藝術家將抽象的數學和材料科學概念轉化為具體可感的藝術品的巧思。它不僅是一件美麗的雕塑，更是一個引導我們思考物質結構和非週期性秩序的有趣案例。金必耀與左家靜巧妙地運用了簡單的串珠技巧，賦予了複雜的科學概念以全新的視覺表達。

想了解更多 串珠 Sierpinski tetrahedron，請造訪 Bridges Math Art Gallery 2014。

© 2025 珠璣科學 |馬凱二十面體

The hydrated diacetates of rhenium

The cover of the inorganic chemistry by J. E. House shows the structure of the hydrated diacetates of molybdenum(II), chromium(II), and rhenium. One can make a very good bead valence sphere model of this molecule containing a metal-metal bond.

Two EMACs

Qian-Rui made these two bead models of EMACs, one with 3 metal cores and the other with 9 cores, last year. The ratio of two types of beads is so small such that the surrounding ligands stop to spiral around the central metal string.

Bead model of the longest EMAC

Qian-Rui made this bead model of the longest EMAC (Extended Metal Atom Chain) for Prof. J. McGrady (Univ. of Oxford) who is an expert on the electronic structures of this class of molecules and is going to visit our department today. In making this model, Qian-Rui chose 10mm beads for both metal-metal and metal-ligand bonds, and 8mm beads for chemical bonds of surrounding ligands. The pitch of the surrounding ligands is slightly larger than the true molecular structure of this molecule. Only a single nylon cord with about 7 meter long is used for this model.





Here is a photo for the giant structure of this molecule hung in the main lobby of our department.

Pentanuclear EMAC

There is a whole family of EMACs with different chain lengths and different metal atoms.
Qian-Rui made this first bead model of EMAC with five metal atoms.


The sizes of beads are 8mm and 6mm, respectively.

Effect of bead sizes on the pitch angle of EMACs

Here I'd to show a few photos of EMACs to how the ratio of two kind of bead sizes on the pitch angles.

1. Correct pitch angle by using 8mm and 6mm beads.


2. Ligands spiral around the central metal string too fast if we use the same kind of beads for both ligands and metal string.


3. No pitch angle if we use 10mm and 14mm beads.

Bead model of tris(bipyridine)ruthenium(II) ion

I mentioned in previous post that I tried to make a beaded model of tris(bipyridine)ruthenium(II) ion (structure is shown below), but didn't succeed.



Somehow, Qian-Rui solved the problem and just showed me the bead model he made for this molecular ion.


This model clearly shows the difference between the planar structural formula and the real 3D structure of a molecule. Chemists are quite used to draw molecules on a paper, but think actually in 3D space. The rationale is the valence shell electron pair repulsion (VSEPR) taught in most general chemistry courses.

Soliton excitation in EMACs

Since right- and left-handed EMACs are mirror images of each other, these two conformatoins should have exactly the same energy. In other words, an infinitely long EMAC has a doubly degenerate ground states. At the absolute temperature T=0, an EMAC can stay either in the left- or right-handed conformation. But at T>0, one may have conformational fluctuations to other excited structures above the ground state. If the barrier to turn left-handed conformation to right-handed conformation is small, soliton excitation may become energetically favorable. An infinitely long EMAC with soliton (or domain wall) consists of three parts: a semi-infinitely long left- and right-handed structures on two sides of polymer and a soliton (a domain wall) with finite lengths in between. It is not easy to determine the size and creation energy of a soliton in an EMAC polymer, though.

Base on my experience with beaded EMACs, it is quite easy to make a soliton in the beaded model as shown in the following picture. So it is reasonable to assume that soliton excitation should be easy in the real, infinitely long EMAC polymers.

Two mor pictures of beaded EMAC

Two more pictures I took at Starbucks Chubei, Hsinchu, yesterday.

Some thoughts on beaded EMACs

Two weeks passed since Chern showed me the first beaded EMAC. Qian-Rui and Chern have further demonstrated that beads can be applied to many more EMACs with different chain lengths and ligands.
I thought, maybe there are more different types of molecules, especially coordination compounds, that can be made with beads. I tried to imagine other molecules I can think of. I tried tris(bipyridine)ruthenium(II) ion tonight. But it didn't work. Right now, I couldn't find any other molecules that can be constructed with beads easily.
It is also quite surprising to me that my group (especially, Qian-Rui Huang and me) has been working on the transport properties of EMACs for a few years. Additionally there is a giant physical model of the longest EMAC compound hung in the main lobby of our deparment, which I've seen almost everyday. But I didn't realize earlier that this class of molecules can be built so faithfully with beads that we have been playing with for four years already.

Two more beaded EMACs

The other two beaded EMACs Qian-Rui made early last week are here. The sizes of beads seem to be 12mm and 8 mm. The pitch angle of the resulting four ligands is so small, so we can almost view them as in parallel with the central metal string in this case. Here Qian-Rui has also managed to add two axial ligands corresponding to the -NCS to two ends of these two molecules.

One more beaded emacs

Qian-Rui Huang made a few more bead models of EMACs using several different colored beads today. Here is one of them:






This model uses five different colors of beads, one for the central metal-metal and metal-nitrogen bonds and the other four colors for four surrounding ligands. So one can easily distinguish helically coiled ligands from the central metal string. The sizes of two different kinds of beads are 12mm and 10 mm, respectively. The pitch angle generated by this choice of beads is a little bit greater than the true molecular pitch angle. Additionally, Qian-Rui has also managed to add two axial ligands with another kind of beads to mimic N-C-S ligands. So each ligand contain three beads.

Bond lengths in the beaded model

In the beaded model of fullerenes that contains only one type of beads, we don't really need to know the relationship between bond length and size of beads to construct a faithful model. But, in molecules such as EMACs, there are at least two types of bond lengths, central metal-metal bonds and ligand bonds, and two types of hybrizations, sp² and d²sp³. It is important to get the correct relation between bond lengths and diameter of beads, in order to get the right pitch angle of EMACs.

In the sp² hybridized carbon atom, we use three spherical beads to mimic carbon-carbon bonds as shown in the left of the following figure. These spherical beads are in contact with each other and the atom is located at the center of three spheres. The relation between bond length and diameter of bead is given by r=1.155a. Similarly, the metal-metal bond lengths for the d2sp3 hybridized atom, is given by r=1.414a.



In the previous post, I gave a simple formula for the pitch angle. But the a and b in the formula should stand for the central metal-metal bond length and the ligand bond length, respectively.

On the pitch angle of a beaded EMAC

I figured out a simple method to estimate the pitch angle of a beaded EMAC that consists of two types of beads, say with diameter a and b (a>b). Beads with size a are used to mimic metal-metal bonds and beads with size b are used to mimic bonds of surrounding ligands. The pitch angle θ can be shown to be approximately given by cosθ=a/(sqrt(3)b) or θ=cos^-1(a/sqrt(3)b). Thus if one use 8mm and 6mm beads to make a bead model of the EMAC compound, the pitch angle can be shown to be θ=cos^-1(8/sqrt(3)*6)= 30. By inspection, one can see that this angle is quite close to that in the beaded model Chuang made. The angle is a little larger than the experimental observation, though.

Three more photos of beaded EMAC

Three more pictures of the beaded EMAC:

Some more pictures of the giant model of the longest EMAC compoound

In the main lobby of chemistry department of National Taiwan University, there is a beautiful model of the longest EMAC compound that was first synthesized by Prof. S.-M. Peng. Here are a few pictures taken by J.-H. Huang.

Comments on using several different sizes of beads in a same beaded structure

In constructing the bead models of the EMACs (extended metal atom chains), we face a new problem, i.e. several apparently different bond lengths in this kind of molecules. Previously, we have been concentrating on the fullerenes which consist of sp²-type carbon-carbon bonds only. The variation of bond length in this type of molecules such as fullerenes is quite small, so in most of molecules we have constructed, we can use beads with same size to get quite faithful structures for them.

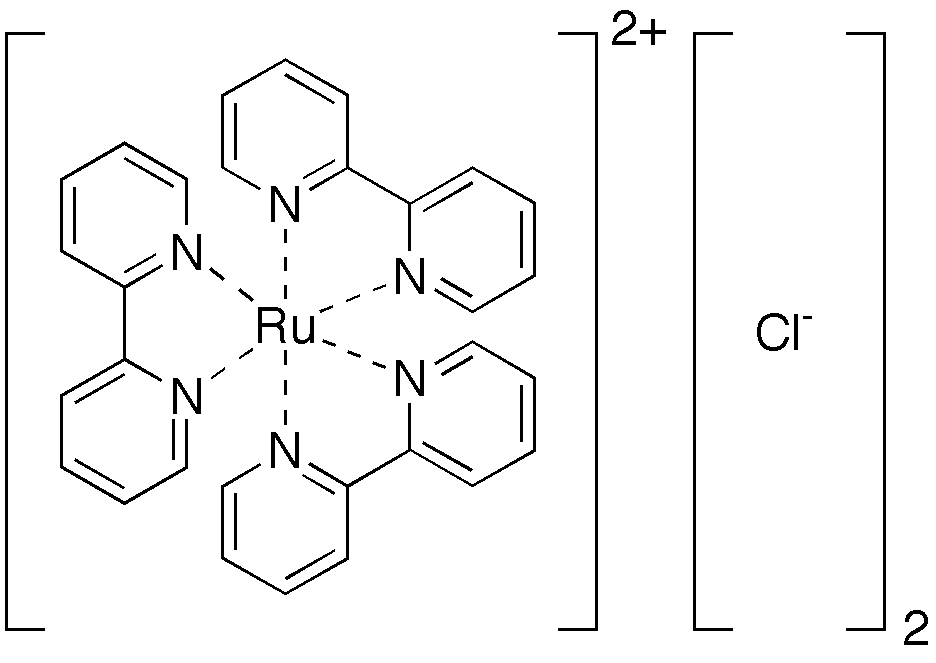
Here EMACs present a new situation since we have two kinds of atoms. In addition to the standard tri-valent sp² carbon and nitrogen in the surrounding ligands, we also have hexa-valent d²sp³ central metal atoms. As we all know, according the VSEPR, trivalent atoms tend to form a planar structure, but hexa-valent atoms prefer to have a locally octahedral structures, i.e. six bonds pointing to the six vertices of a octahedron. The lengths of central metal-metal bonds and the surrounding ligand bonds are quite different. For instance, in the famous tri-nuclear metal complexes [M₃(dpa)₄Cl₂] where M = Co^II, Ni^II , Co^II, and so on. The lengths of the central metal-metal bonds are about 0.23 ~ 0.25 nm. But the bond lengths of the surrounding carbon-carbon bonds are only about 0.14 nm. The bond lengths for bonds between central metal atoms and donor atoms (nitrogen) are about 0.2 nm. So it is not possible to construct this kind of molecules with only one type of beads, we have to use at least two or three types of beads to represent these bonds in order to get a faithful representation of this kind of molecules.

In the bead model Chuang made for the longest Emacs, he used two types of beads, 6mm beads for the bonds in the surrounding ligands and 8mm beads for the central metal-metal bonds and the metal-nitrogen bonds. The difficulty for making bead model for EMACs comes from the central metal-metal bonds. Unlike the typical carbon-carbon bonds, where we need to thread the fish line through every small beads (carbon-carbon bonds) twice; here we need to thread each large beads (metal-metal bonds) four times. This makes the weaving difficult. I am glad that Chuang succeeded in making it. The resulting bead model is surprisingly stable and just like a rigid rod, especially for the central metal string. This can also be understood as a beautiful realization of VSEPR for the central metal string.

One can also see that the four surrounding ligands spiraling around the central metal string beautifully. But the only problem is that the ligands spiral around the central metal string too fast. One can easily understand this because the size of smaller beads in this structure is too big. The ratio of bond length for metal-metal bond vs metal-nitrogen bond vs ligand bond is 0.24 nm : 0.20nm : 0.14 nm = 1.2: 1.0: 0.7. The size of large beads should be almost twice of that of small beads. The two sizes Chuang used is 0.8 cm: 0.6cm. I have never seen beads with a size 0.7cm in local stores in Taipei. So maybe a good option for making EMACs is to use either two types of beads with 1.2 cm and 0.8 cm or three types of beads with 1.2 cm, 1.0 cm and 0.8 cm, respectively. The pitch for the surrounding ligands may be still shorter than the true molecule, but should be closer.

Another problem for making bead model of EMACs is how to construct two axial ligands which are not in any loop of molecular graph of the corresponding EMACs. Up to now, all of the bead models we have been making have all beads belonging a particular loop. The simplest method is simply ignoring them. This is how Chuang handled it. Additionally, one can also use a small bead to stop the bead that represents axial ligand from falling off.

Some useful structural information from Jinn-Tsair Sheu, Cheng-Chen Lin, Ito Chao, Chih-Chieh Wang and Shie-Ming Peng*, "Linear trinuclear three-centred metal-metal multiple bonds: synthesis and crystal structure of [M₃(dpa)₄C1₂] [M = Ru^II or Rh^II, dpa = bis(2-pyridy1)amido anion]" Chem. Commun. 1996, 315.

Fig. 1, ORTEP view of[R^II₃(dpa)₄Cl₂] along the metal-metal bond axis.


Table 1, Structural comparison of [M₃(dpa)₄C1₂] trinuclear metal complexes

Bead model of the longest Emac (Extended Metal Atom Chain)

Extended metal atom chains (Emacs) refer a family of molecules that consist of a central metal atoms with metal-metal bonds and four surrounding ligands. My colleague Shie-Min Peng is a pioneer in this field.

The shortest emacs contain three central metal atoms such as triCobalt emacs, [Co₃(dipyridylamido)₄Cl₂]⁺, as shown in the following figure:
.
(Dimitrios A. Pantazis, Carlos A. Murillo and John E. McGrady, Dalton Trans., 2008, 608)

Originally, I don't think beads are suitable for making molecular model for this kind of molecules. But Chern Chuang proved that I was wrong. Today, right after I came back to my office, Chern gave me the first bead model of the longest emacs with 11 Nickel atoms that has ever been synthesized.