Shing-Tung Yau's visit (丘成桐)

Famous mathematician, Shing-Tung Yau (Winner of Fields Medal 1982 and Wolf Prize in Mathematics 2010), and some of his friends (Prof. Mu-Tao Wang 王慕道, Math. Dept., Columbia university; Prof. I-Liang Chern, 陳宜良, Math. Dept., National Taiwan Unversity; another one I don't know) came to see the beadworks in our chemistry department yesterday morning. He seemed to enjoy these mathematical beadworks and asked me a few questions like whether these nontrivial structures have been really synthesized etc. ...

I told him I would feel honor to give him any model in the display case if he like it as a gift. He chose the bead model of P-type TPMS with (2,0).

P-surface with (1,0) vector

Chern made this (1,0) P-type triply periodic minimal surface with 4mm beads many years ago. I might have posted it long time ago, but forgot to make a suitable keywords for that post, so I couldn't find anywhere in this blog.
Chern used a different color coding for this bead model, i.e. orange for hexagons and black and organe alternatively for octagons. Since there is no bead which is not in octagons, one would get a single color bead model by using the color coding we adopted typically.

(1,1) and (2,0) P-type Triply Periodic Minimal Surfaces

It would be nice to compare two P-type TPMSs, one with the Goldberg vector (1,1) and the other with (2,0), together. Here the Goldberg vector, (m,n), denotes the separation between two neighbored octagons. In this sense, (1,1)-P-TPMS is similar to C60, while (2,0)-P-TPMS to C80 in the spherical space.

Pagodane （塔烷）

According to the wiki:

A pagoda （塔） is the general term in the English language for a tiered tower with multiple eaves common in Nepal, India, China,Japan, Korea, Vietnam, Burma and other parts of Asia. (source: wiki)

About twenty years ago, H. Prinzbach was able to synthesize an organic compound with a skeleton which resembles a pagoda by a 14-step sequence starting from isodrin. Thus he named the compound pagodane （塔烷）.

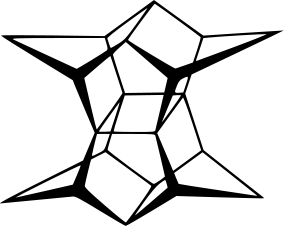
I just knew this molecule from the book "Molecules With Silly Or Unusual Names" by Paul W. May the other day. So here is the bead model of this interesting molecule.

Three Kekule structures of C60

D. Vukicevic and M. Randic have figured out all possible distinct resonance (or Kekule) structures a few years ago. According them, buckminsterfullerene has 12500 Kekule structures grouped in 158 isomorphic classes. They also give a complete list of all these 158 non-isomorphic Kekuke structures in a recent paper entitled "Detailed Atlas of Kekulé Structures of the Buckminsterfullerene", in the book, "The Mathematics and Topology of Fullerenes".

This is very convenient if we want to make any particular resonance form of C₆₀. We can simply look at the Schlegel diagrams given in this paper, and pay attention to the single and double bond pattern as we bead. Here are three bead models for Kekule structures No. 134, 135 and 136 as shown in their paper.

Adamantane (金剛烷)

I made a bead valence sphere model of adamantane (chemical formula C₁₀H₁₆), which is a cycloalkane and also the simplest diamondoid.

Neopentane

Neopentane, also called dimethylpropane, is a double-branched-chain alkane with five carbon atoms. (from wiki)

Cyclohexane conformation

I made a bead valence sphere model of cyclohexane, C₆H₁₂, which seems to reproduce all important structural features of this molecule.

Fullerane: C60H60

Fullerane is any hydrogenated fullerene or fully saturated fullerene. For instance, the fully saturated C₆₀ is C₆₀H₆₀. One can make a faithful valence sphere model of C₆₀H₆₀ with beads. The 150 beads in this model represent 300 valence electrons (240 from carbon and 60 from hydrogen) in this molecule.

Bead VSM of tetrahedrane

I should forget another platonic alkane, the tetrahedrane. The shape of this molecule based on the valence sphere model is just like 10 spheres close packed in a tetrahedron. Which models, valence sphere model or ball-and-stick model, is closer to the true shape of a tetrahedrane molecule?

Bead VSM of dodecahedrane

In principle, we can make the valence sphere model for any molecule with beads. But in practice, it is a little bit hard to thread the Nylon cord through a bead structure with tetravalent bonds, which are common for most molecules though.
But anyway, I made a bead VSM of dodecahedrane, C₂₀H₂₀.

Bead VSM of cubane

I just made a bead VSM (valence sphere model) of cubane (C₈H₈) by myself. The structure looks neat to me. Every valence electron pair is faithfully represented by a big bead, purple for CC bond and pink for CH bond. Small beads which have no chemical meaning are used to bind the pink beads to the central carbon cube. I didn't distinguish CC bonds from CH bonds. In principle, electron pairs responsible for these two types of chemical bonds should have different momenta. So they should have different sizes of charge clouds.

Bead VSM of methane, ammonium, water, and hydrogen fluoride

There is no doubt that tetravalent molecules such as methane occupy an important place in the chemical bond theory.
In 1865, German chemist August Wilhelm von Hofmann made the first stick-and-ball molecular models of methane in lecture at the Royal Institution of Great Britain. It is planar!

Then, 1872, van't Hoff, then a graduate student, learned of a possible tetrahedral arrangement of the valence bonds of carbon, proposed by the Russian chemist Alexander Butlerov in 1862. He later made a set of 3-D paper models of tetrahedral molecules.

Following Prof. H. Bent's recipes, Qing Pang (龐晴) of TFGH (北一女) made several bead valence sphere models (bead VSM) for tetravalent molecules with the formula AX_nE_m, where n+m=4, n is the number of bond electron pairs and m is the number of lone electron pairs. Here she didn't use the Windsor's knot to end the Nylon thread, instead she used simply tiny beads to cap the terminal beads of this kind of tree-like structures. Also, she use blue beads to represent bond electron pairs and yellow beads long electron pairs. You can see bead model exactly realizes the valence sphere model of Bent. I will show other bead VSM (made by Qing Pang) of molecules with several centers later.

Super Buckyball

Mr. Hwang took this picture of my group the next day after I had the workshop last month.

Tangent sphere model of ethane

Using beads, one can make a faithful representation of the so-called valence sphere model (VSM) or tangent sphere model for a molecule proposed by Prof. Henry Bent in the 60s. In this model, each valence electron pair in a molecule is represented by a sphere. Its diameter is determined by the de Broglie wavelength of the corresponding electron, λ = h/p, where p is its momentum and h is the Planck constant.

Here is the first bead VSM (BVSM) of ethane (C₂H₆) made by Qing Pang (龐晴) of the Taipei First-Girls High School (北一女). She used the so-called Windsor-knot technique (雙活結) to bind beads that are not parts of loops in a molecular graph. For simplicity, she used beads of the same size to build the BVSM of ethane. This is equivalent to making the assumption that all valence electrons have the same momentum. The paper below the bead model is from the manuscript entitled "Approximate Molecular Electron Density Profiles. I. Construction" that I got from Prof. Bent last month.

BTW, Prof. Bent has just published a new book entitled "Molecules and the chemical bond" which is the first book-length sequel of his early articles on tangent sphere model last year. If you want to know more about the tangent sphere model, you should read the book or the original articles published in J. Chem. Edu.
You can read parts of this book at the google book.

1. Bent, H. A. J. Chem. Edu. 1965, 40, 446.
2. Bent, H. A. J. Chem. Edu. 1965, 40, 523.
3. Bent, H. A. J. Chem. Edu. 1967, 42, 308.
4. Bent, H. A. J. Chem. Edu. 1967, 42, 348.
5. Bent, H. A. J. Chem. Edu. 1968, 44, 512.
6. Bent, H. A. J. Chem. Edu. 1967, 45, 768.

beaded vase

Bang-Rui's mother knew my hobby of making beaded molecules. So she gave me a beautiful beaded vase she made. It is basically a pillar-shaped C₈₄ with the top surface removed.

Here is a bead model of pillar-shape C₈₄ I made before.

The other two smaller fullerenes in the same homologous series are C₆₀ and C₇₂.