Tetrahedral C28 and related structures

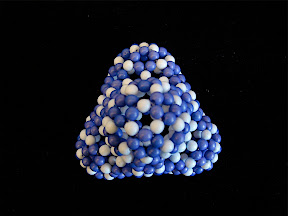
There are only three tetrahedral fullerenes with number of carbon atoms less than that of buckyball. They are C₂₈, C₄₀, and C₄₄, respectively. The spiral code for the smallest tetrahedral fullerene, C₂₈, is [1 2 3 5 7 9 10 11 12 13 14 15]. Following this code, we can easily make its bead model using the standard figure-eight stitch. We can see that, in this molecule, there are 12 pentagons, 3 in a group located at a vertex, and 4 hexagons located on the four faces of the tetrahedron. If we replace these pentagons by heptagons, we get a tetrapod-like structure, in which tri-pentagon vertices become tri-heptagon necks as shown in the following figure.

Using these tetrapods as building blocks, we can get the following diamond-like structure. In fact, this is exactly the structure Mr. Horibe put in the postcard. OK, if we start from other tetrahedral fullerenes such as C₄₀ and C₄₄, we can find out a lot more diamond-like structures.

Hyperbolic "buckyball" with octagons

I played with carbon tetrapods described in the Diudea and Nagy's book last weekend and discovered quite accidentally that it is possible to make another type of hyperbolic "buckyball" with neighbored nonhexagons separated by only one CC bond. Particularly, all nonhexagons in this structure are octagons. So this one is different from another hyperbolic "buckyball" made of heptagons and hexagons, or simply heptagonal buckyball. The skeleton of this structure is the same as the heptagonal "buckyball". But each unit cell, which consists of two connected tetrapods, has 96 carbon atoms. I am not sure if people have mentioned this kind of hyperbolic "buckyball" or not.

Heptagonal "buckyball", C168 (This model was given to Prof. Sonoda as a gift when I was invited to Japan for a series of talks and workshops.):

(photo by Dancecology)

Octagonal "buckyball", C96:

More carbon tetrapods

In the appendix of "Periodic Nanostructures", M. V. Diudea and C. L. Nagy gave an extensive list of tetrapod-like structures of carbon nanotubes. Here are some bead models based on the structures listed in the book.

C84 with three and four heptagonal holes

As I said in the previous post, one can puncture holes on a C₈₄ and use the resulting structures as basic units for building larger graphitic structures. Here I show two C₈₄-derived bead models with three and four holes surrounded by heptagonal.

The Schlegel diagram and a simple beading path for three-hole structure can be worked out easily.

Similarly, here is the Schlegel diagram and a beading path for a four-hole (tetravalent) unit.

Of course, one can use these building blocks to make many interesting structures. I am planning to make a dodecahedron consisting of 20 tetravalent units. It is not hard to see the angle between two holes in a unit is about 109 degree which is very close to 108 degree for the inner angle of a pentagon. So one can expect that these units should be happily fitted in the resulting dodecahedron without too much distortion.

C60 vs C168

One can view C60 or a buckyball as the simplest graphitic sheet embedded in a sphere with every pentagon connected to five other pentagons by only single carbon-carbon bonds. In this sense, C168 can be viewed as the "buckyball" in the hyperbolic space with every heptagon connected to seven other heptagons by only single carbon-carbon bonds.

I made a bead model of C168 that consists only of one tetrapod (half unit cell). So only 84 carbon atoms are included in this structure. The structure I posted previously contains 5 unit cells.

Molecular tetrapod!

Based on the Lenosky's work on the carbon nanostructure derived from periodic minimal surface (as told by Chuang Chern), I found that it is possible to make carbon nanotetrapod. Although I soon discovered (through googling) that this kind of tetrapod has been studied by a Korean group a few years ago (PRL 2003), I still found this kind of structures intriguing.

From Craft Projects

From Craft Projects