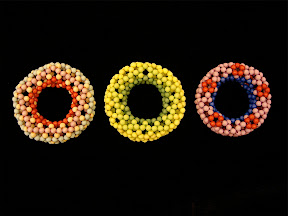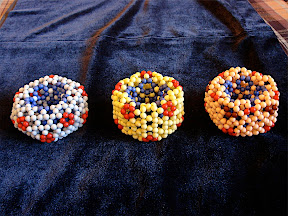More beaded fullerenes or spheroids

Here is some more beaded spheroids I made (90 10mm beads were used.):

C₇₀ top view

From The Beaded Mo...

C₇₀ side view

From The Beaded Mo...

C₇₈ top view

From The Beaded Mo...

C₇₈ bottom view

From The Beaded Mo...

Another three isomers of Torus 200

Torus 200 has another three isomers, two are chiral and the other is achiral as shown below. Since two chiral molecules are mirror image of each other, so I only stitch one of them.

Chiral Torus 200

From The Beaded Mo...

Achiral Torus 200

From The Beaded Mo...

All three in a row

From The Beaded Mo...

My desktop

From The Beaded Mo...

Another achiral carbon nanotorus: C200

A smaller beaded toroids with 300 beads. This corresponds to nanotorus with 200 carbon atoms. Note that this molecule and all previous molecules have exactly 10 heptagons located periodically in the inner rim and 10 pentagons in the outer rims.

Since the beads are in fact chemical bonds in the molecule, and each carbon has three CC bonds, we have the simple rule for calculating the relation between the number of beads and the numbers of carbons:

the number of carbons = the number of beads *3 /2

From The Beaded Mo...

Three Carbon 240 isomers: T240

I found it is also easier to see the difference between these three isomers from a different view angle. Here is the side view of the previous three isomers

From The Beaded Mo...

Chiral Toroid 240: T240

The previous two C240 isomers both have an inversion center. Hence, both of them are achiral, which means the mirror of the molecule is identical to itself. However, it is not difficult to find out it is possible to generate a chiral toroid by slight shifting of pentagons on the outer rim by one unit cell. Here is the result of the chiral isomer of the previous two structures.

Larger Beaded Toroids: Carbon 240

Here are another examples of beaded toroids, C240. These two structures contain 360 beads each, thus 360 CC bonds. The details of construction are pretty complicated. At present time, I will only show the pictures for the finished structures first.

The Simplest Beaded Toroids

In addition to spherical object such as C₆₀, it is also possible to construct structures with spheroidal and toroidal shape by beading. The most difficult part of the construction is that we have to figure out the correct connectivity between different beads. I will discuss this issue later.

Here are the simplest beaded toroids with 120 carbon atoms I made.

The first molecule has D_5d symmetry.



Another C120 isomer is a chiral molecule.

The Beadiful Fullerenes

A few weeks ago, when shopping with my wife in one of local stores which supplies all kinds of craft stuffs in Taipei, I was soon attracted by those beaded 3-D beadworks in the store. Standing in front of these cute artworks, I started to ponder about the possibility to use these beads to model the structure of molecules. But what kind of molecules? Due to the richness of chemical bonds, I know I could not use beads for every possible bond types. With only a little thought, I realized that beads are perfect for constructing molecular models of carbon fullerene, C₆₀, higher fullerenes, and nanotubes. More importantly, it seems that even much more complicated structures with shapes like spheroids and toroids can be made from the beads. To check my preliminary thought, I decided to buy some necessary materials to start with. These include three packs of 10mm beads and a roll of fishing line.

As my first molecular beading project, I chose the simplest fullerene, C₆₀, which is a truncated icosahedron consisted of 60 carbon atoms. At the beginning, I don't know anything about the weaving technique. Fortunately, my wife has some experiences. So under her guidance, I learned the basic technique, later I know that this technique is the so-called right-angle weaving. Here is the first beaded C60 I constructed:

(Beaded ball with 10mm beads.)

After I finished my first beaded molecule, I soon realized that the molecule I made is not really the so-called buckyball, C₆₀ with beads corresponding to the atoms. In fact, the beaded ball I made is composed of 90 beads, instead of 60 beads! What went wrong? If we examine carefully the structure of the beaded ball, we can see that there are four beads surrounding each bead! This is not allowed in the trivalent carbon compounds as we know. Each carbon atom can only have three neighbors! It is not hard to see that every bead in the beaded ball form triangle with two near-neighbored beads. There are 60 this kind of triangles in a ball. Now we have the clue to resolve the puzzle, the beads in the beaded molecules do not correspond to the atoms, instead, they represent chemical bonds! There must be a carbon atom located at the center of each triangle. So, we can say that the beaded molecules are the bond-representation of a real molecule, instead of the commonly used atom-representation.

I made more beaded buckyballs with 4mm beads later: