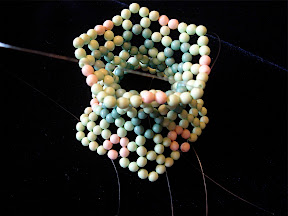As I have mentioned that the details of the beading procedure for creating a fullerene molecule describable by a spiral should be completely determined by the sequence of pentagons and hexagons. Once this sequence is given, then we can just carry out the weaving process by making the 5 or 6-bead group using the RAW according the recipies. Sound simple, right. But we still need to know the sequence in order to make the fullerene we intend to create. Fortunately, the complete list of all possible isomers for fullerenes in the range C
20 to C
50 and isolated-pentagon isomers of fullerenes in the range C
60 to C
100 are tabulated in Fowler's "An Atlas of Fullerenes". Instead of giving the whole sequence of 5- and 6-gons. Fowler also gives another simplified notation for the sequence of 5- and 6-gons in the spiral. Since there are exactly twelve pentagons in a fullerene, and the others are hexagons, therefore we only need to know the positions for the pentagons in the spiral.
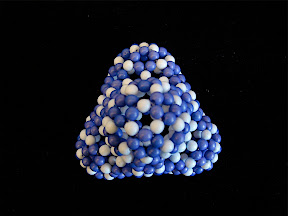
Here I will illustrate his notation with two simple examples. The first one is an isomer of C
80, Fowler's 80:7 isomer (the 7th isomer out 7 isolated-pentagon isomers of C
80), with the spiral code, 1 8 10 12 14 16 28 30 32 34 36 42. According this spiral code, I have to make a pentagon first, then 6 hexagons, and then a pentagon, hexagon, pentagon, and so on, in a clockwise spiral. Finally a C
80 is created. In the process of making this fullerene, I don't need to worry about the connectivity or geometry, the resulting beaded C
80 is in good agreement with the actual geometry of C
80 due to the repulsion between different beads.
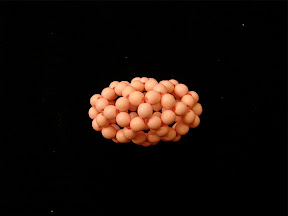
Another one I made is isomer 50:24 with spiral code 1 2 3 4 7 12 17 22 24 25 26 27, which is an isomer of C
50. The shape of this isomer looks like a bean or cocoon.