Since the last month of 2011, I started to work on the so-called Sierpinski buckyballs or superbuckyballs, which belong to a particular family of fullerenes created by treating C60s as supernodes and carbon nanotubes as superbonds. Using this idea, an unlimited number of hierarchical super-structures of sp
2-hybridized (3-coordinated) carbons can be constructed. Before this task was really started, I have managed to build some simpler structures such as super-triangle, super-tetrahedron, and other related structures. With the experience, I firmly believed in the feasibility of creating bead models of much larger superbuckyballs.
But
it is too tedious to construct bead models for this kind of super-structures, especially the so-called C60xC60, alone. So I designed a modular approach to build these models collaboratively. I told a few chemistry teachers, especially Dr. Chou (周芳妃), at a local high school, The Taipei First-Girl School (TFGH), about this structure. They were glad to try this idea out together. The results are two beautiful superbuckyballs (or C60xC60) made by 6mm and 12 mm beads, respectively. Both of the structures were on public display for the anniversary of TFGH and a simultaneous event of the TFGH's 30-year alumni reunion. Alumni association of TFGH kindly supported the whole project. Dr. Tsoo was one of alumni that year, that was why we got supported from them.
Later on, I made another bead model of C60xC60 for the JMM held in San Diego about two years ago (Jan. 2013).
I used the photo of the giant bead model students and I made in the JMM description though.
I met Chern (莊宸) in the meeting. We discussed the structural rules for this family of compounds. Particularly, I commented on that the particular model I made cannot be constructed by Zometool. After returning back to Cambridge, MA, Chern solved the problem by carefully puncturing holes along certain symmetry axes in order to be consistent with the Zometool requirements.
Yuan-Jian Fan (范原嘉) then proved Chern's idea by building a virtual C60xC60 super-buckyball with the zometool construction software, vZome, which was kindly given to us by its author, Scott Vorthmann, a few years ago. With everything ready, a few enthusiastic students from the theoretical chemistry group of the National Taiwan University started to build the first zometool super buckyball after the Chinese new year.
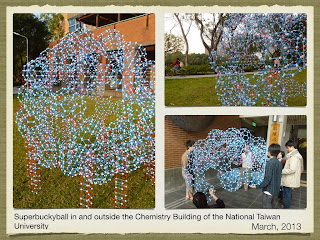
Soon, a number of practical issues on the construction of a real zometool model of C60xC60 super-buckyball appeared. The first issue is the structural stability against gravity. The original neck structures (shortest situations) designed by Chern consisted of a number of octagons were too weak and simply cannot hold the whole structure due to its own weight. Another issue is still weight, without extra stands, the southern hemisphere of super-buckyball constructed by zometool simply cannot hold the northern hemisphere. Finally, how to put those parts on top without scaffold is also a question. All these problems were solved beautifully by Yuan-Jia Fan. Of course, local dealer, Helen Yu, of Zometool in Taiwan is also helpful. She always responded us with the necessary zometool pieces upon our requests in a very short time. So, we can have the first zometool sculpture of C60xC60 erected in the NTU campus around mid-March.
Chern then proposed to Paul Hildebrand to have a family-day activity for the 2013 Bridges which will be held in Enschede that year. Paul agreed to provide us with the necessary materials. At the family day, we got more help from a few Bridges participants and their family members from Taiwan. These included Profs. Liu (劉柏宏) and Tung-Shyan Chen (陳東賢). Without them the final C60xC60 structure couldn't be finished in such a short period.
In addition to the construction of huge zometool superbuckyball, Chern also presented
a small bead model to the Bridges meeting as shown in the following pictures based on the same construction rule he designed. Another bead model in his right hand is an edge-elevated dodecahedron assembled from fifty C80s, twenty for the vertices of dodecahedron and thirty for the elevated edges. The idea for making this one is similar to C60xC60.
I brought them back to Taiwan and put them on exhibition in the NTU Chemistry Museum for about a year until the last July when Chern got an email from George Hart asking him about the possibility of donating this small C60xC60 model for
MoSAIC (Mathematics of Science, Art, Industry, and Culture) traveling exhibition. In the email, George commented on this model as " having the right combination of artistic expression, mathematical content, and practical transportability".
